- 第39届CCF中国数据库学术会议在威海成功举行
- CCF数据库专业委员会2023年第三次常委扩大会议
- 第40届CCF中国数据库学术会议在贵阳成功举行
- 第38届CCF中国数据库学术会议在昆明成功举办
- 第37届CCF中国数据库学术会议在华中科技大学成功举行
- 第 37 届 CCF 中国数据库学术会议(NDBC 2020) 征文通知
- 山东大学承办第36届中国数据库学术会议
- 第35届中国数据库学术会议在大连海事大学成功举行
- 数据科学与工程教育论坛申办指南
- 第33届中国数据库学术会议(NDBC 2016)征文通知
- 第32届全国数据库学术会议
- 中国计算机学会第28届中国数据库学术会议总结
- 祝贺DSE期刊入选中国计算机学会推荐期刊
- 祝贺DSE期刊被EI数据库收录
- DSE精选文章 | 基于众包的困难搜索任务设计与任务集构建 A Crowd-powered Task Generation Method for Study of Struggling Search
- DSE精选文章 | Top-k Competitive Location Selection over Moving Objects
- DSE精选文章 | 基于GPU的完全并发动态超空间哈希 GPU-based Dynamic Hyperspace Hash with Full Concurrency
- DSE精选文章 | 基于高质量种子识别的面向静态和动态网络的多重局部社区发现 Multiple Local Community Detection via High-Quality Seed Identification over Both Static and Dynamic Networks
- DSE APWeb-WAIM 2020精选特邀论文特刊
- DSE精选文章 | 用于分布式图数据存储的工作负载自适应流数据分区器 A Workload‑Adaptive Streaming Partitioner for Distributed Graph Stores
- DSE精选文章 | SUMA:高效的支持OWL 2 DL的查询回答系统 SUMA:A Partial Materialization-based Approach to Scalable Query Answering in OWL 2 DL
- DSE精选文章 | 基于群体用户聚集的最优路径查询
- DSE精选文章 | 面向组合优化问题的图学习综述 Graph Learning for Combinatorial Optimization: A Survey of State-of-the-Art
- DSE精选文章 | 大规模图数据上的关键词搜索综述 Keyword Search on Large Graphs: A Survey
- 喜讯|DSE被ESCI收录
- DSE简介
- DSE编委会
- DSE论文
- 2022年度VLDB暑期学校暨20周年特别论坛成功举办
- VLDB Summer School 2022 报名工作启动
- 2021年度VLDB暑期学校成功举办
- VLDB Summer School 2020重磅来袭!
- 2020年度VLDB暑期学校成功举办
- 2019年度VLDB暑期学校
- VLDB summer school 2018
- VLDB Summer School 2017回顾
- VLDB Summer School 2016 回顾
DSE精选文章 | 基于群体用户聚集的最优路径查询
Data Science and Engineering (DSE)是由中国计算机学会(CCF)主办,数据库专业委员会承办,施普林格·自然(Springer Nature)集团出版的开放获取(OA)期刊。本篇文章精选自DSE最新一期发文,得到中新赛克赞助文章处理费。
文章介绍
近年来,随着互联网尤其是移动互联网的发展,基于位置的服务(Location based Services (LBS))在人们日常生活中的位置导航、路径规划、物流车辆管理、道路规划等方面的发挥着越来越重要的作用。路径规划作为基于位置服务中重要的一项服务,是地理信息系统以及时空数据库等领域中的重要的研究课题。传统的路径规划的主要目标是查询从起点到终点的最优路径,指标方面主要关注的是消耗时间、路径代价或者燃油消耗等,不能够满足人们日益丰富的查询需求,例如路径查询中对访问位置的类别有次序要求、涉及多用户会面情形的查询要求等。如何在多用户查询场景下满足这些用户更为丰富的查询需求,是路径规划中具有实际意义和价值的一个巨大挑战。
针对以上问题,我们研究了一种最优次序路径(OSR)查询(又称最优顺序路径查询)的变体,叫做会面的最优组次序路径查询(OSR-G),目标在于为一组查询用户找到最优会面点或者最优会面兴趣点,使得这组查询用户的所有的查询路径中的最大路径代价是最小的,这些用户从各自的出发点出发并依次访问一系列的兴趣点(例如:加油站,餐馆等),最终在最优会面点会面。OSR-G查询不仅考虑了多用户的会面查询场景而且能够满足每个用户的访问兴趣点带次序的需求。
本文首先提出了一个精确算法(基于OSR的算法,称为OSRB算法)作为解决OSR-G查询问题的基本方法(作为其他方法的对比),OSRB利用现有的 OSR算法(E-OSR)检查会面兴趣点中所有的兴趣点来为每个用户计算其到会面点的最优路径。为了改进OSRB算法,本文在设计新算法时引入了剪枝策略,避免检查所有的候选会面点,提出了圆滤(CF)算法以及一个下界剪枝算法。其中,圆滤算法利用一种性质过滤掉一些不必要检查的会面点。而下界剪枝(LBP)算法,最短路径下界剪枝算法(LBP-SP),采用了下界来剪枝掉大量的非最优会面点来缩减搜索空间。本文证明了了任意最优次序路径代价下界都可以嵌入本文提出的的下界剪枝算法框架来解决OSR-G查询问题。
为了处理规模较大的 OSR-G查询,在下界剪枝算法的基础上,本文设计了一个近似算法,近似点选(APS)算法,来加速OSR-G查询。APS算法有很好的近似比保证。实验结果显示圆滤算法和下界剪枝算法性能要优于OSRB算法并且有很好的剪枝效率,LBP-SP 算法在精确算法中性能表现最好。还有,提出的近似算法在运行时间上要明显优于提出的精确算法并且具有很好的近似比。
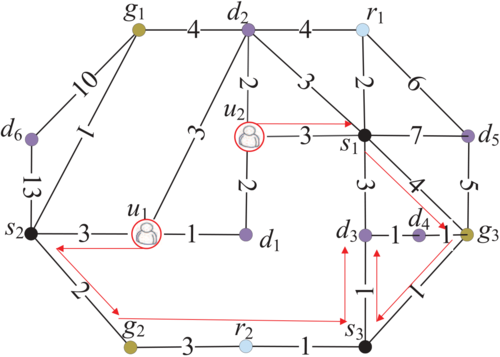
图 1. 一个路网图:查询用户所在点{u1,u2},超市兴趣点{s1,s2,s3},餐馆兴趣点{r1,r2},加油站兴趣点{g1,g2,g3},候选会面点集{d1,d2,...,d6}
实验效果
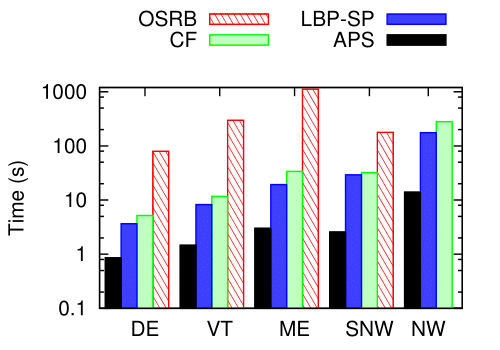
图2展示了不同数据集上本文提出的查询算法的运行时间对比。可以看到,CF和LBP-SP算法查询性能要优于OSRB算法,近似算法APS是所有算法中查询速度最快的。这是因为CF和LBP-SP算法都运用了剪枝策略,而OSRB算法却简单地检查了所有的候选会面点。LBP-SP算法比CF算法查询要快主要取决于其有更高的剪枝效率,同理APS算法查询速度是最快的。
图 2. 不同数据集上查询算法运行时间对比
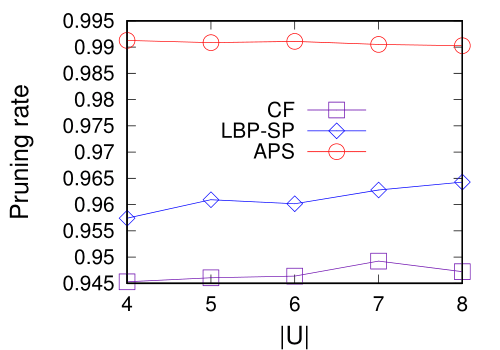
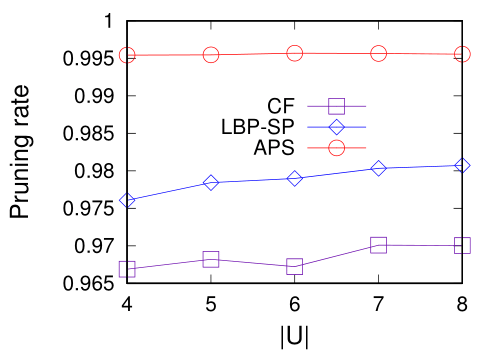
图3对比了随查询用户数变化下不同算法的剪枝效率。可以看到,从剪枝效率高低来看,APS>LBP-SP>CF。随着查询用户数的增长,三种算法的剪枝效率都保持相对稳定(变化不超过1%)。不管查询用户有多少,会面代价仅取决于有最大路径代价的用户。因此,查询用户个数对算法剪枝效率影响不大。其次,剪枝效率越高,算法运行速度越快,这与图2中的结果是对应的。
(a) VT dataset (b) ME dataset
图 3. 查询用户数和查询算法的剪枝效率对比
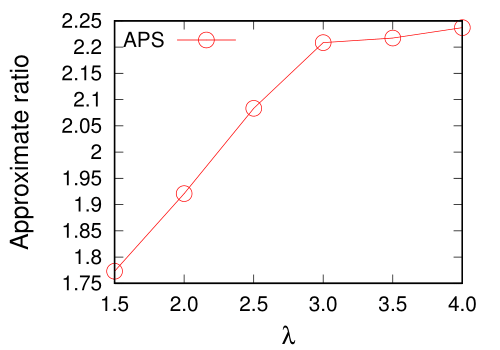
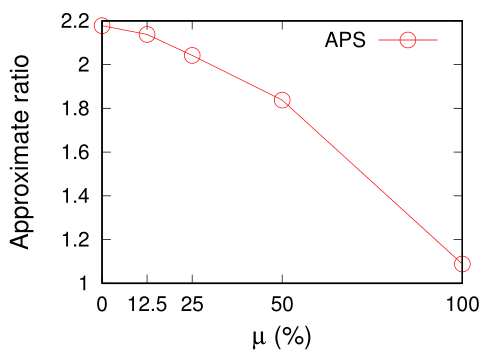
图4展示了λ和μ对APS算法近似比的影响。如图4(a)所示,随着λ(APS剪枝参数)的增加,APS算法的近似比大幅提升(意味着解质量下降);到λ=3.0时,近似比逐渐平稳。在图4(b)中,而随着μ(查询用户中执行精确算法的比例)的增加,近似比从2.2下降到接近1(意味着查询结果质量上升)。
(a) (b)
图 4. λ和μ对APS算法近似比的影响
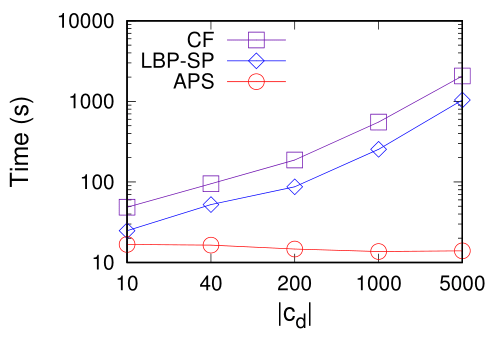
图5展示了NW数据集下候选会面点集合大小对查询算法的性能影响。从图5(a)可以看到,确切算法(CF和LBP-SP)的查询时间随着候选会面点的增加而增加。这是因为要检查的候选会面点数目增加了。近似算法APS却恰恰相反,随着候选会面点增加,APS算法查询时间是先下降(这是由于其剪枝效率足够高并且随着候选会面点增加有提升)后上升(这是由于APS算法的剪枝效率已经接近收敛)。图5(b)中,三个算法的剪枝效率都随着候选会面点的增加的逐渐增加直至收敛。
(a)运行时间 (b)剪枝效率
图 5. NW数据集下候选会面点集合大小对查询算法的性能影响
总结
本文形式化提出了会面的最优组次序路径查询(OSR-G),目标在于为一组查询用户找到一个最优会面点以及每个查询用户的最优访问路径,使得这个查询用户组中的每个查询用户访问一系列兴趣点后能够尽快的会面。OSR-G查询不仅能够满足多用户会面的需要,而且能够满足这些查询用户在会面前各自访问一系列兴趣点的个性化查询需求。
本文对会面的最优组次序路径查询进行了系统化的研究。本文提出了OSRB算法来作为解决OSR-G问题的算法的对比方法。为了改进OSRB算法,本文设计新算法时引入了剪枝策略,提出了圆滤(CF)算法和一个下界剪枝算法(LBP-SP)。本文证明了任意最优次序路径的下界都可以嵌入本文提出的下界剪枝算法框架中作为新的下界剪枝算法。为了有效处理规模较大OSR-G查询,本文在下界剪枝算法框架的基础上提出了最优点选算法(APS)算法,APS算法不仅查询速度快,而且还有较好的近似比保证。
本文工作可能为未来工作带来几个新的研究方向,例如:基于会面点的前 k 最优组次序路径查询,可以为查询用户组查询前 k 组最优路径为查询用户组提供更多的选择;更有效的最优组路径下界,最优组路径下界存在改进空间,可以考虑构建一些的索引更好地来估算最优组路径的下界。
作者简介
陈波,中山大学计算机学院硕士研究生。主要研究方向为时空数据库查询。
朱怀杰,中山大学计算机学院副研究员,2012年在东北大学计算机科学系获得硕士学位,2018年在东北大学计算机科学系获得博士学位。主要研究领域为空间数据库、数据隐私保护、社交网络等。
期刊简介
Data Science and Engineering(DSE)是由中国计算机学会(CCF)主办、数据库专业委员会承办、施普林格 自然(Springer Nature)出版的Open Access期刊。为了迎合相关领域的快速发展需求,DSE致力于出版所有和数据科学与工程领域相关的关键科学问题与前沿研究热点,以大数据作为研究重点,征稿范畴主要包括4方面:(1)数据本身,(2)数据信息提取方法,(3)数据计算理论,和(4)用来分析与管理数据的技术和系统。
目前期刊已被ESCI与SCOPUS收录,CiteScore2020为4.9,在Computer Science Applications领域排名#181/693(73rd Percentile)。稿件处理费由赞助商中新赛克(Sinovatio)承担,欢迎大家免费下载阅读期刊全文,并积极投稿。
原文链接:https://link.springer.com/article/10.1007/s41019-021-00153-5